Dynamic Thinking
Say that a main() program has called fib(5).
The diagram shows the activations, their parameters (in blue),
and their return values (in red).
Pick an activation and study how the activations below it
correspond to the code.
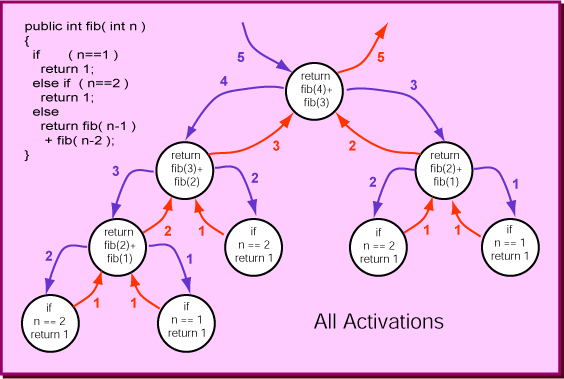
The diagram labeled All Activations shows how each activation (except for the base cases) is supported by two other activations.
To see the dynamic sequence of activations, repeatedly click on the diagram. A solid circle represents an activation that is currently computing or waiting for a result to be returned. When an activation is shown as a dotted circle, it has finished its computation and is "history". It is no longer on the activation chain.
At any time in the execution of fib(5) the activations
that have not yet finished their computation (because they are waiting for a value)
form a single chain.
There is never more than one activation chain.
The activation chain bends left and right, but there is always a single successor
and a single predecessor for each link (except for the first activation and for
the base cases.)
